How to align 3D point clouds with ICP?

from sklearn.neighbors import NearestNeighbors
import numpy as np

def nearest_neighbor(src_points: np.array, dst_points: np.array):
'''
Find the nearest neighbor between the point clouds

Args:
src_points(np.array): The coordinates of the first point cloud.
dst_points(np.array): The coordiantes of the second point cloud.

Return:
(np.ndarray): Distances from the src_points to the closest points in dst_points
(np.ndarray): Indices of the nearest points in the point clouds.
'''
neigh = NearestNeighbors(n_neighbors=1)
neigh.fit(dst_points)
neigh_dist, neigh_ind = neigh.kneighbors(src_points, return_distance=True)
return neigh_dist.ravel(), neigh_ind.ravel()

Introduction

Point set registration is the process of finding a spatial transformation that align two discrete set of data points. This can be used to map new measurements to a know dataset or to perform pose estimation.

Multiple methods of point alignment exists, in this article we will cover the implementation in python of Iterative Closest Point, an algorithm of point cloud alignment that finds best-fit transforms to move one point cloud so that it is aligned with another.

Implementing ICP

The implementation of ICP has been added to this google colab document.

The first step of ICP is to calculate the closest point from the second point cloud to the first one.

Then it calculates the best transform that maps points between two point clouds. To do so, the transformation of the Iterative Closest Point is performed in 2 steps, first calculating the center of mass of the first point cloud and shifting the center of mass of those corresponding points and as a second step, the optimal rotation is calculated using singular value decomposition(SVD).

What the singular value decomposition does is break down any linear transformation that the matrix of the original point cloud represents into three geometrical transformations: a rotation or reflection, followed by a coordinate-by-coordinate scaling, followed by another rotation or reflection.

The following code is creating the three transformations:

def calculate_best_transform(src_points: np.array, dst_points: np.array):
'''
Calculates the best transform that maps points between two point clouds.
The cross-covariance matrix between the point clouds is calculated, then
rotations and translations are extracted using singular value decomposition.

Args:
src_points(np.array): The coordinates of the first point cloud.
dst_points(np.array): The coordiantes of the second point cloud.

Returns:
(np.array)(src_points.shape[1]+1)x(src_points.shape[1]+1) homogeneous transformation matrix that maps src_points on to dst_points
(np.array)(src_points.shape[1]xsrc_points.shape[1]) rotation matrix
(np.array)(src_points.shape[1]x1) translation vector
'''
# translate points to their centroids
centroid_src_points = np.mean(src_points, axis=0)
centroid_dst_points = np.mean(dst_points, axis=0)
# compute covariance
cov = compute_cross_covariace(src_points, dst_points, centroid_src_points, centroid_dst_points)
# rotation matrix
U, S, Vt = np.linalg.svd(cov)
R = np.dot(Vt.T, U.T)
# get number of dimensions
m = src_points.shape[1]
# special reflection case
if np.linalg.det(R) < 0:
Vt[m-1,:] *= -1
R = np.dot(Vt.T, U.T)
# translation
t = centroid_dst_points.T - np.dot(R,centroid_src_points.T)
# homogeneous transformation
T = np.identity(m+1)
T[:m, :m] = R
T[:m, m] = t
return T, R, t

Once the transformations are created they can be applied to the source points iteratively, making them be more closer to the destination points in each iteration. The following code can be used to perform the iteration:

def icp(src_points: np.array, dst_points: np.array, init_pose: np.array=None, max_iterations: int=20, tolerance: float=0.001):
'''
Finds best-fit transform that maps points in src_points on to points in dst_points
using Iterative Closest Point method.

Input:
src_points(np.array): The coordinates of the first point cloud.
dst_points(np.array): The coordiantes of the second point cloud.
init_pose(np.array): homogeneous transformation
max_iterations(int): exit algorithm after max_iterations
tolerance(float): convergence criteria

Return:
(np.array)(src_points.shape[1]+1)x(src_points.shape[1]+1) homogeneous transformation matrix that maps src_points on to dst_points
Euclidean distances (errors) of the nearest neighbor
number of iterations to converge
'''
# get number of dimensions
m = src_points.shape[1]
# make points homogeneous, copy them to maintain the originals
src = np.ones((m+1, src_points.shape[0]))
dst = np.ones((m+1, dst_points.shape[0]))
src[:m,:] = np.copy(src_points.T)
dst[:m,:] = np.copy(dst_points.T)
# apply the initial pose estimation
if init_pose is not None:
src = np.dot(init_pose, src)
prev_error = 0
for i in range(max_iterations):
# find the nearest neighbors between the current source and destination points
distances, indices = nearest_neighbor(src[:m,:].T, dst[:m,:].T)
# compute the transformation between the current source and nearest destination points
T,_,_ = calculate_best_transform(src[:m,:].T, dst[:m,indices].T)
# update the current source
src = np.dot(T, src)
# check error
mean_error = np.mean(distances)
if np.abs(prev_error - mean_error) < tolerance:
break
prev_error = mean_error
# calculate final transformation
T,_,_ = calculate_best_transform(src_points, src[:m,:].T)
return T, distances, i

Graphic Example

For instance, consider the bellow two 3D objects, a face and a sphere. All points of the face belong to a discrete set of data point and all points of the sphere belong to another discrete set of data point.

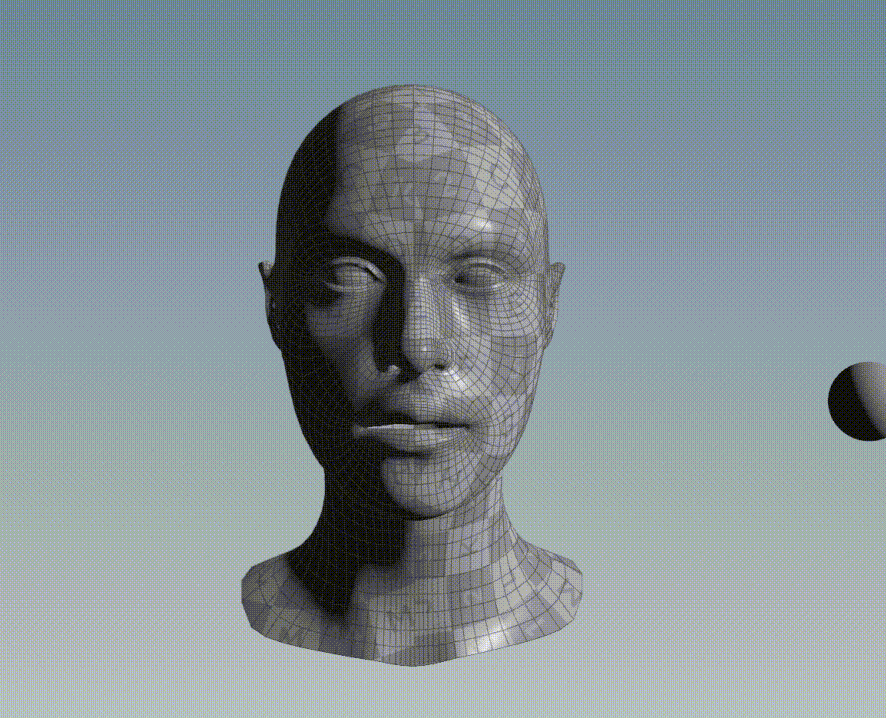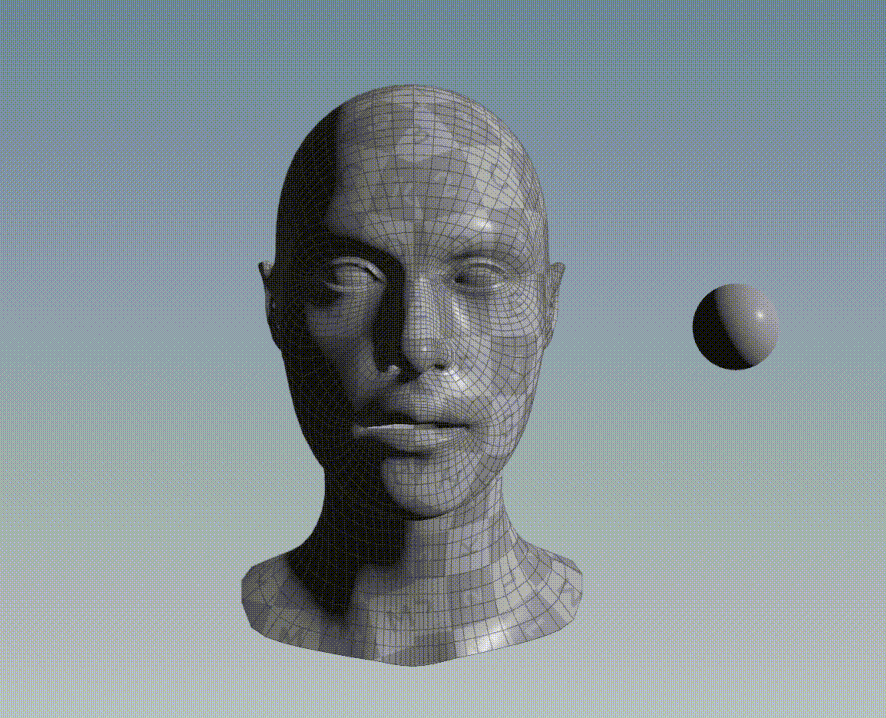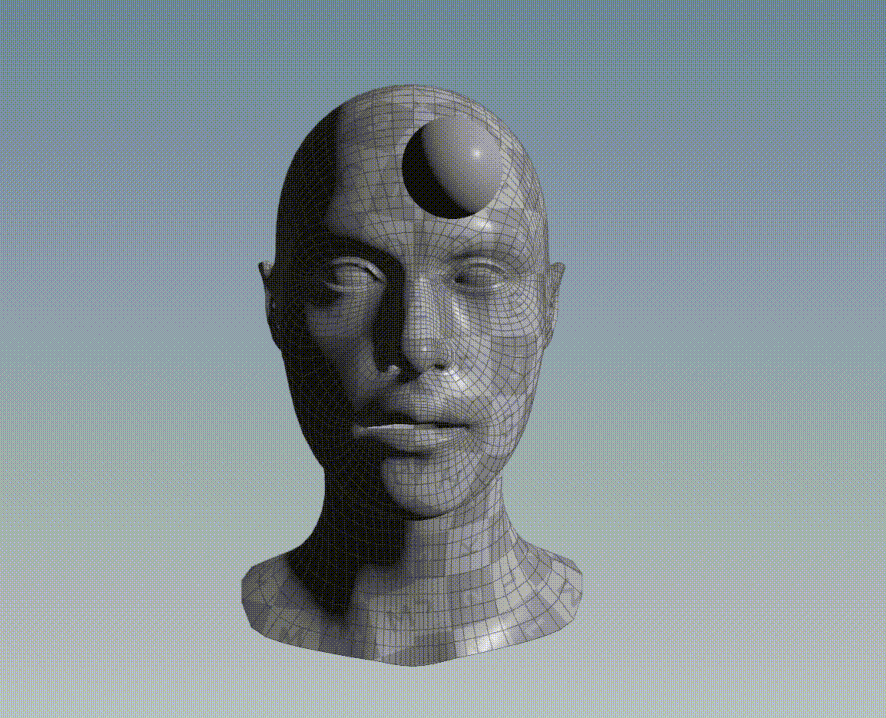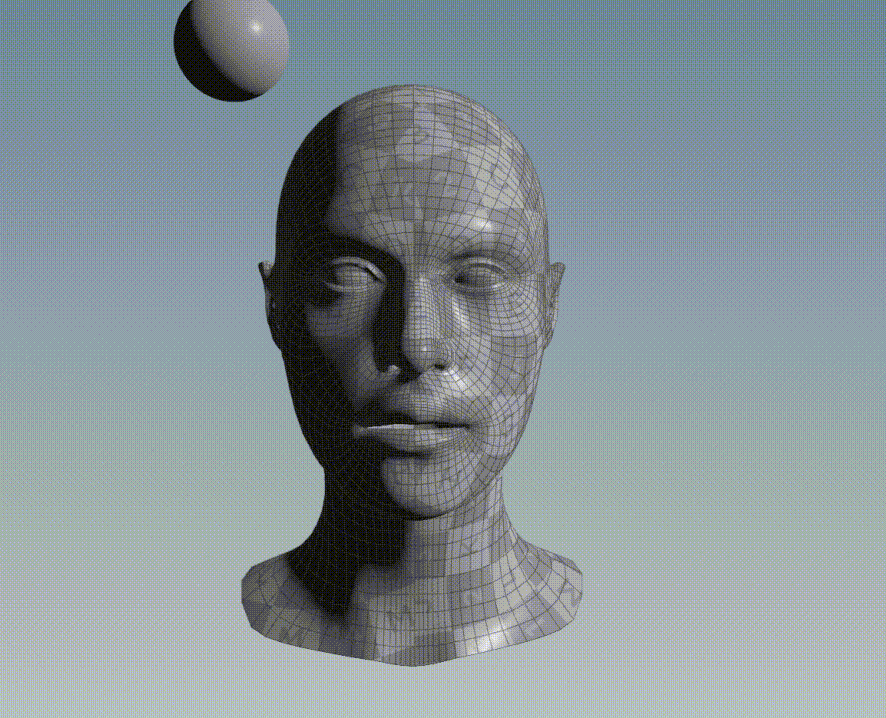
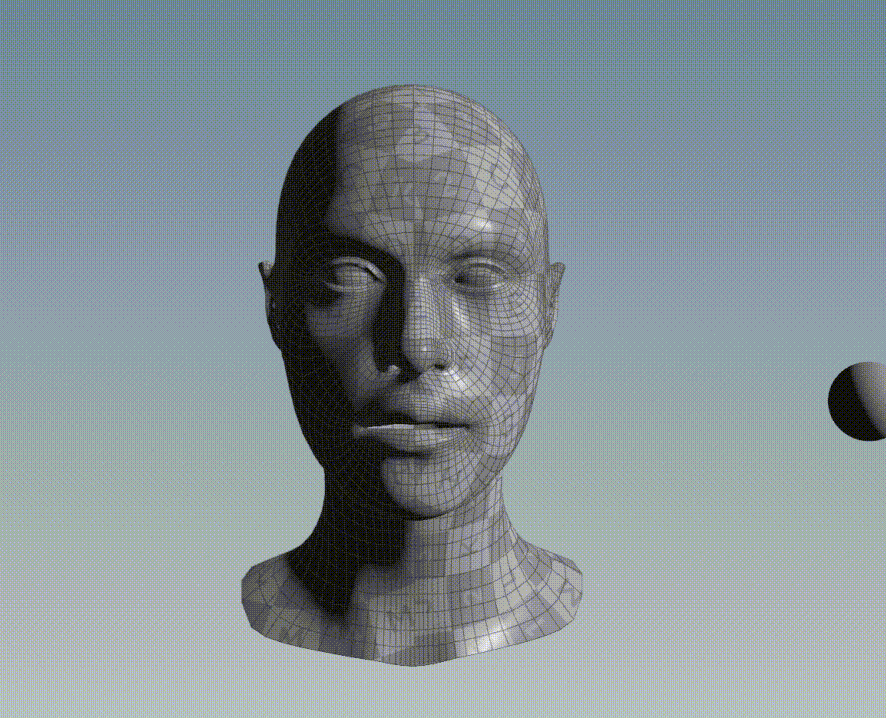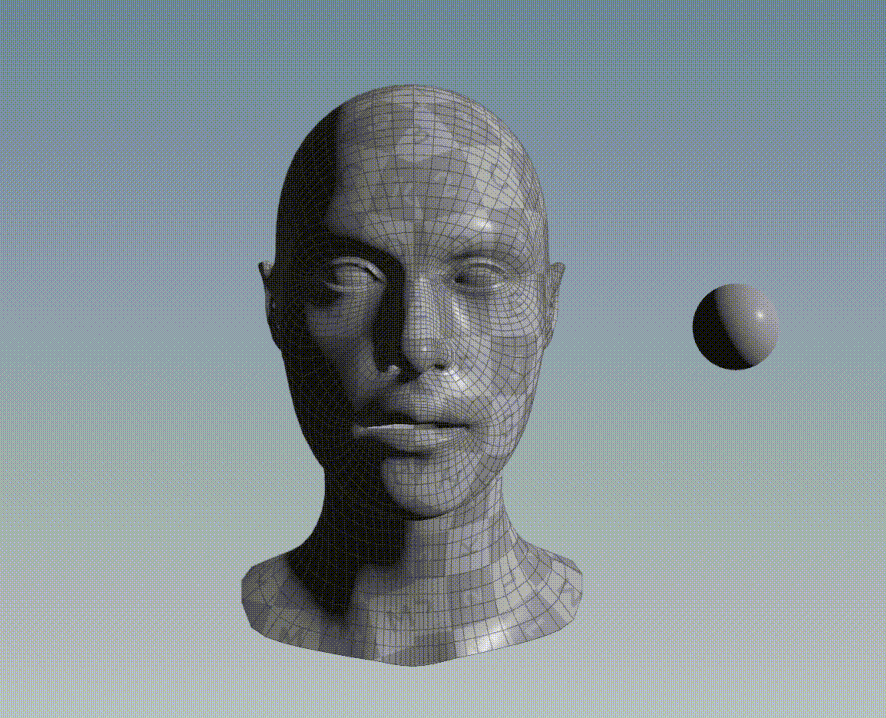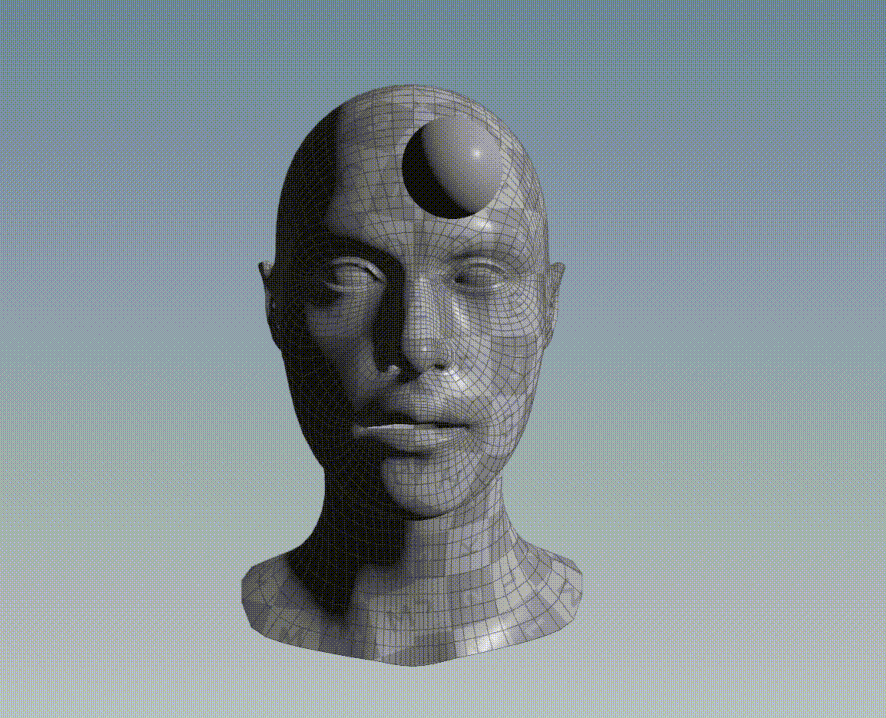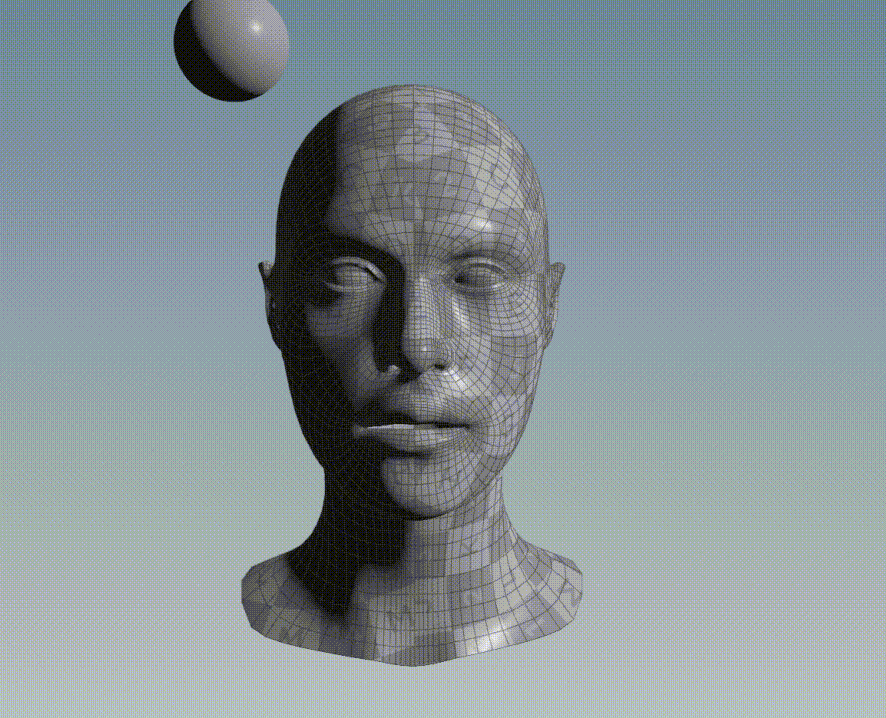
If ICP is applied to align the points of the sphere to the points of the face, the following result is obtained:

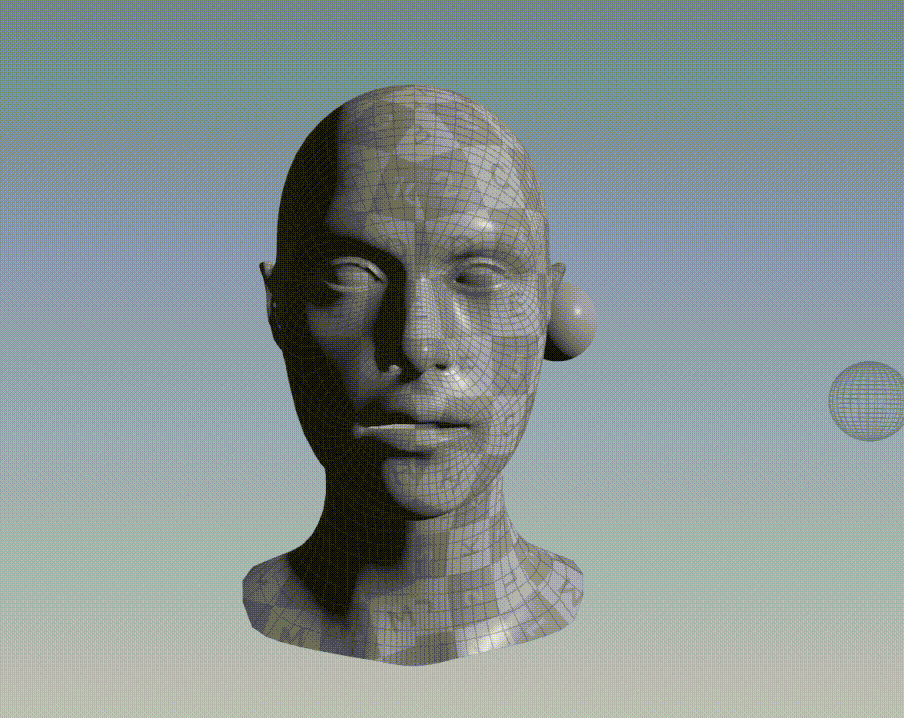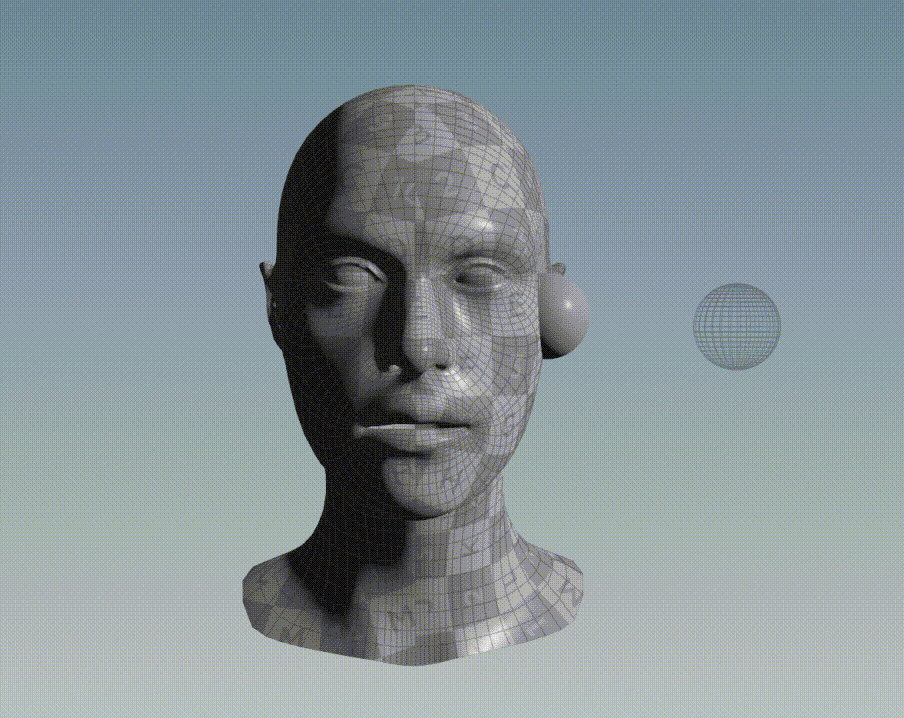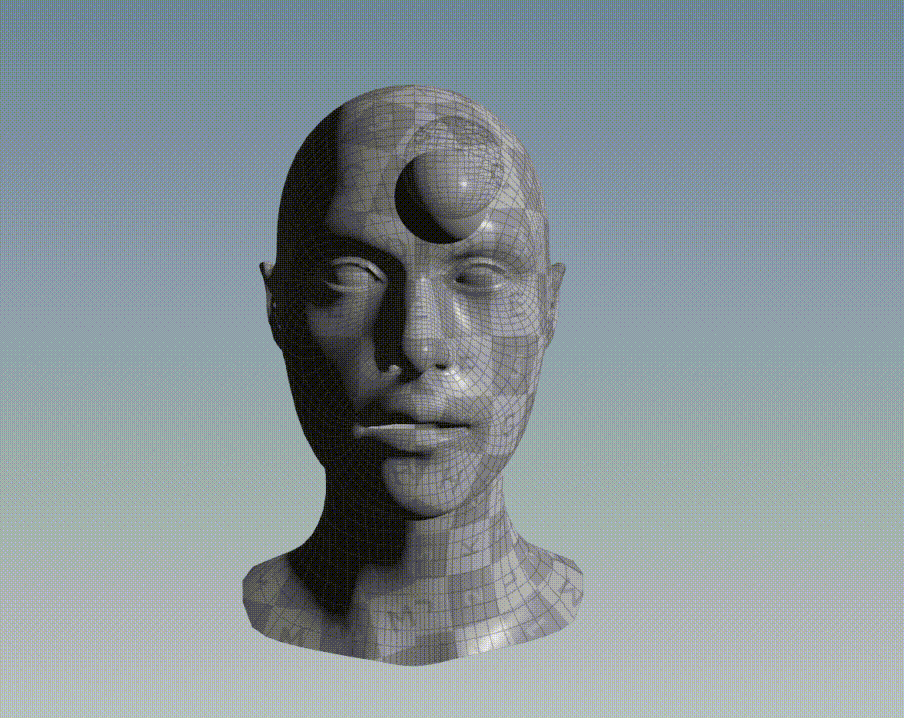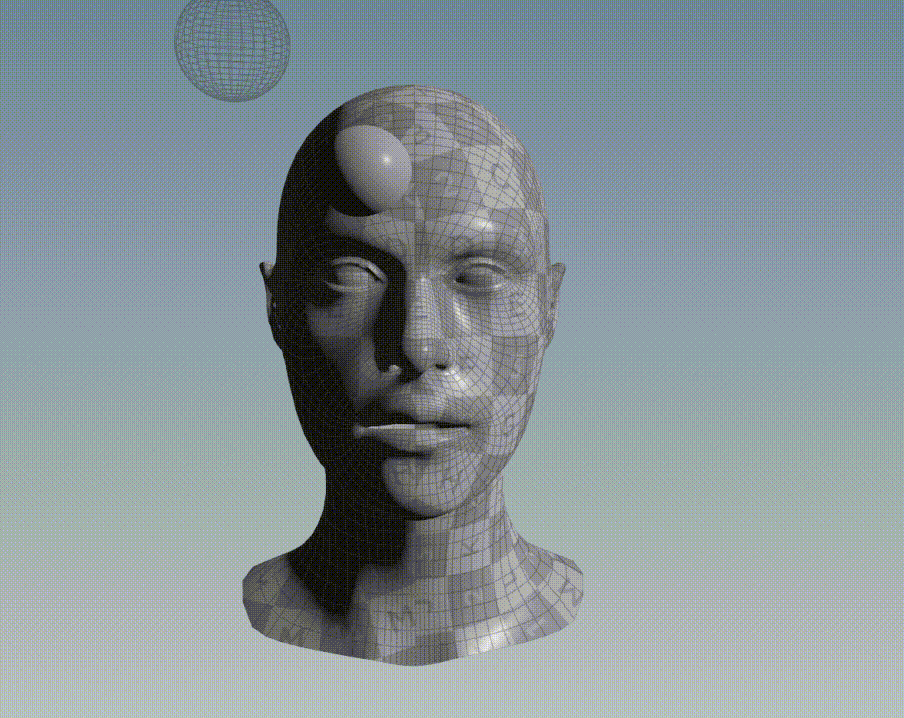
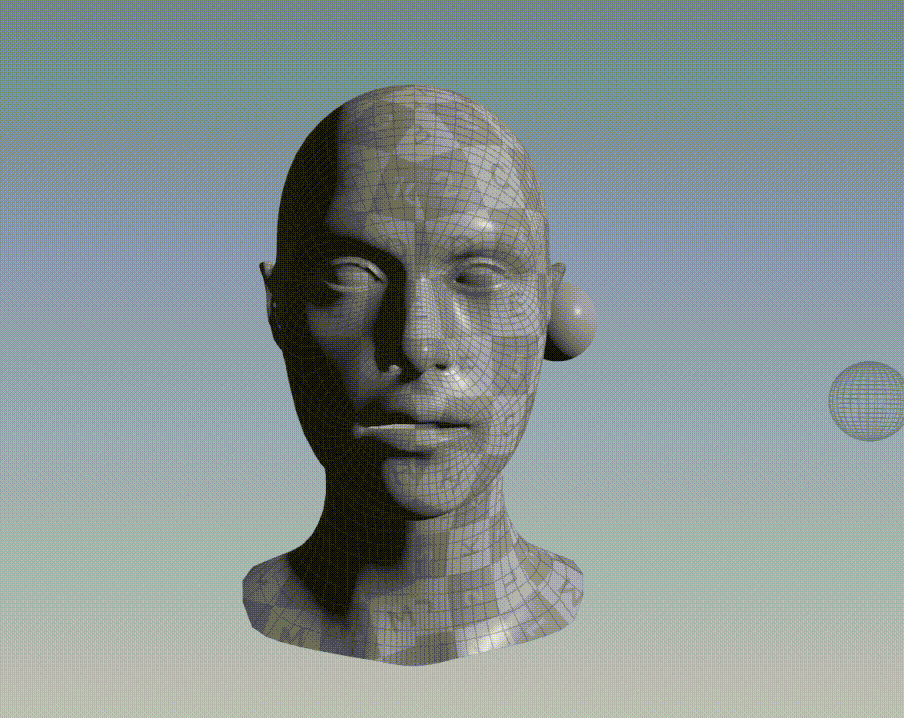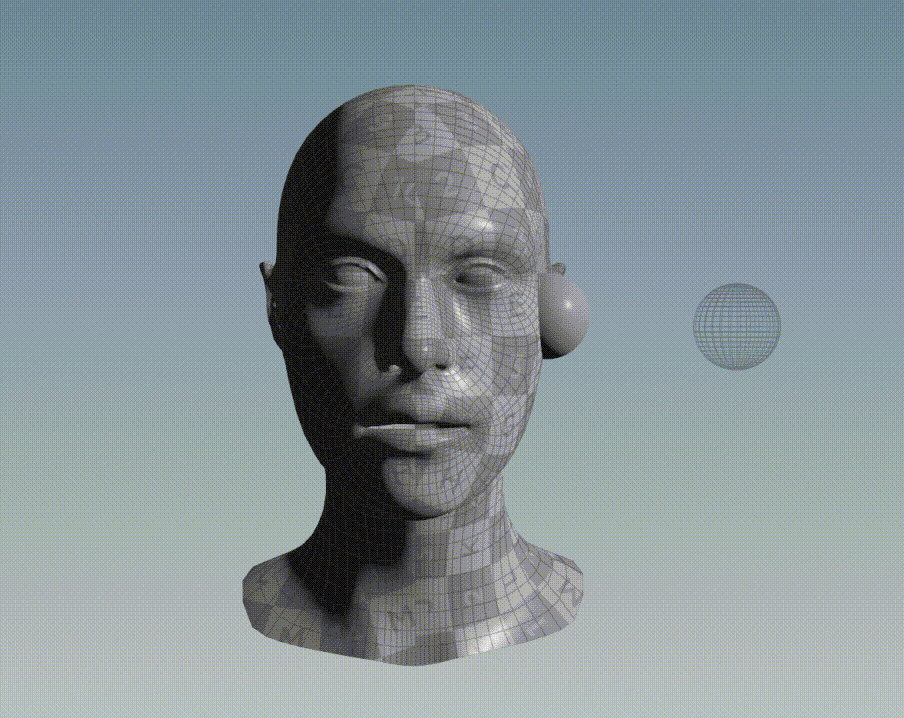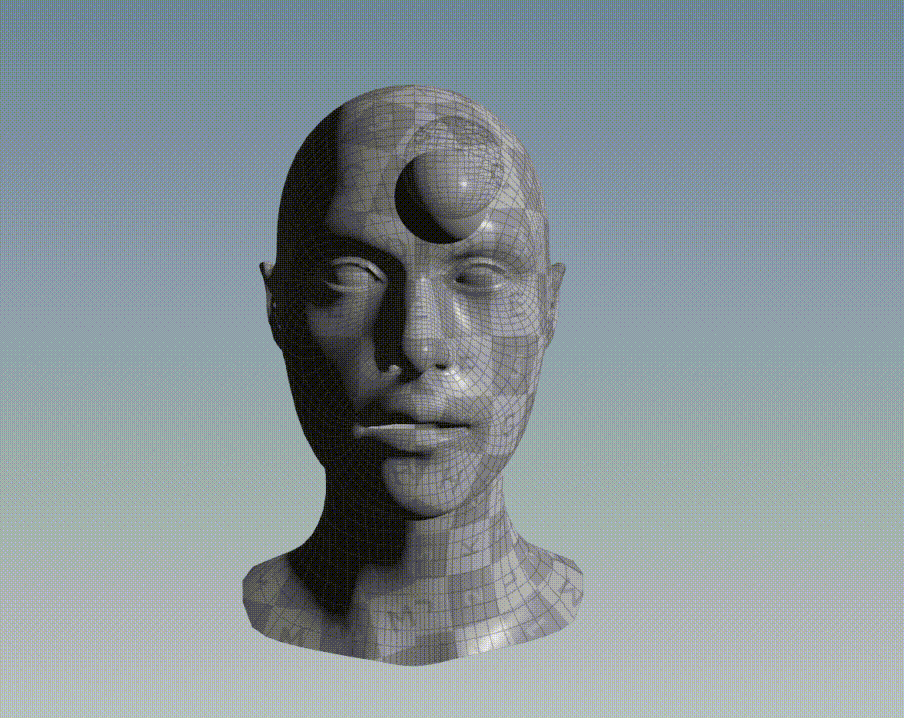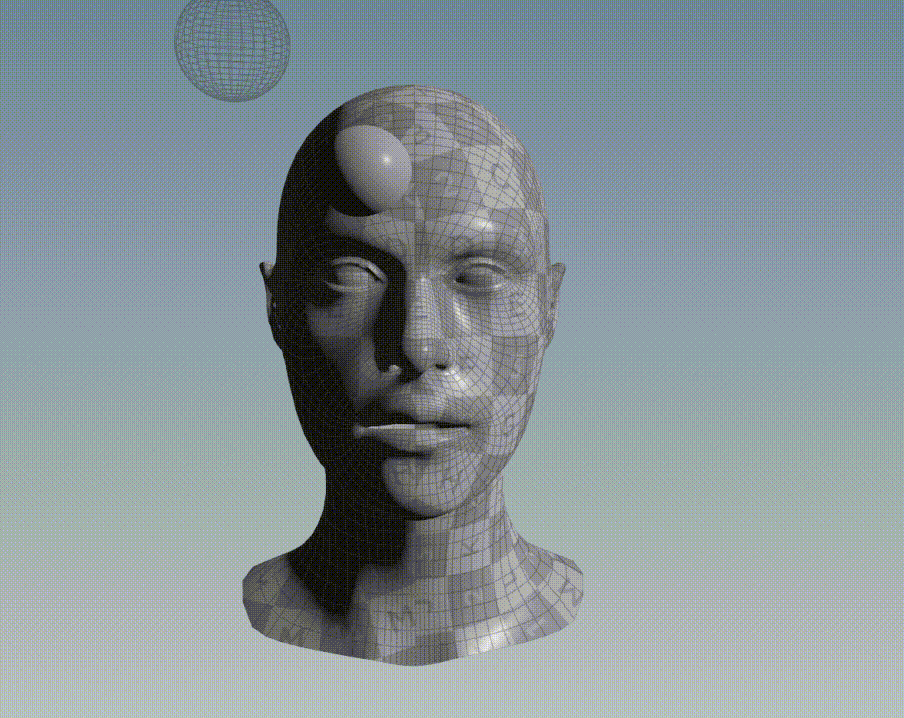
Post can also be found in medium